Skip to contents

Optimization & Traces

optimization_traces.Rmd

This vignette covers the available optimizers, step size control, and how to visualize optimization traces.

Optimizers

The optimizer class defines the optimization strategy and is initialized by taking an objective function, start value, and learning rate. Available optimizer are:

  • Gradient descent with OptimizerGD
  • Momentum with OptimizerMomentum
  • Nesterovs momentum with OptimizerNAG

Creating an optimizer is done by (let’s use an x value that works well):

obj = obj("TF_GoldsteinPriceLog")
opt = OptimizerGD$new(obj, x_start = c(0.22, 0.77), lr = 0.01)

With these value set, optimization is done by calling $optimize() with the number of steps as argument:

opt$optimize(10L)
#> TF_GoldsteinPriceLog: Batch 1 step 1: f(x) = 0.9158, x = c(0.219, 0.7186)
#> TF_GoldsteinPriceLog: Batch 1 step 2: f(x) = 0.4217, x = c(0.211, 0.6549)
#> TF_GoldsteinPriceLog: Batch 1 step 3: f(x) = -0.6741, x = c(0.1844, 0.5649)
#> TF_GoldsteinPriceLog: Batch 1 step 4: f(x) = -0.9819, x = c(0.2182, 0.5224)
#> TF_GoldsteinPriceLog: Batch 1 step 5: f(x) = -0.9876, x = c(0.2992, 0.5105)
#> TF_GoldsteinPriceLog: Batch 1 step 6: f(x) = -1.1018, x = c(0.2625, 0.3598)
#> TF_GoldsteinPriceLog: Batch 1 step 7: f(x) = -2.168, x = c(0.3405, 0.4107)
#> TF_GoldsteinPriceLog: Batch 1 step 8: f(x) = -2.1246, x = c(0.3448, 0.3898)
#> TF_GoldsteinPriceLog: Batch 1 step 9: f(x) = -1.3408, x = c(0.4093, 0.4614)
#> TF_GoldsteinPriceLog: Batch 1 step 10: f(x) = -2.1225, x = c(0.3729, 0.3911)

Calling $optimize() also writes into the archive of the optimizer and also calls $evalStore() of the objective. Therefore, $optimize() writes into two archives:

opt$archive
#>                   x_out                x_in                    update
#>                  <list>              <list>                    <list>
#>  1: 0.2189909,0.7185977           0.22,0.77 -0.001009067,-0.051402328
#>  2: 0.2109802,0.6548741 0.2189909,0.7185977   -0.00801070,-0.06372357
#>  3: 0.1844147,0.5648984 0.2109802,0.6548741   -0.02656552,-0.08997572
#>  4: 0.2182254,0.5223500 0.1844147,0.5648984    0.03381065,-0.04254834
#>  5: 0.2992118,0.5105193 0.2182254,0.5223500    0.08098642,-0.01183078
#>  6: 0.2625368,0.3597982 0.2992118,0.5105193   -0.03667496,-0.15072102
#>  7: 0.3405450,0.4106795 0.2625368,0.3597982     0.07800819,0.05088128
#>  8: 0.3448264,0.3897982 0.3405450,0.4106795  0.004281407,-0.020881313
#>  9: 0.4092595,0.4613701 0.3448264,0.3897982     0.06443313,0.07157191
#> 10: 0.3728515,0.3910876 0.4092595,0.4613701   -0.03640808,-0.07028256
#>       fval_out    fval_in    lr step_size         objective_id momentum  step
#>          <num>      <num> <num>     <num>               <char>    <num> <int>
#>  1:  0.9157526  1.2102644  0.01         1 TF_GoldsteinPriceLog        0     1
#>  2:  0.4217145  0.9157526  0.01         1 TF_GoldsteinPriceLog        0     2
#>  3: -0.6741307  0.4217145  0.01         1 TF_GoldsteinPriceLog        0     3
#>  4: -0.9818620 -0.6741307  0.01         1 TF_GoldsteinPriceLog        0     4
#>  5: -0.9876309 -0.9818620  0.01         1 TF_GoldsteinPriceLog        0     5
#>  6: -1.1017546 -0.9876309  0.01         1 TF_GoldsteinPriceLog        0     6
#>  7: -2.1680122 -1.1017546  0.01         1 TF_GoldsteinPriceLog        0     7
#>  8: -2.1245834 -2.1680122  0.01         1 TF_GoldsteinPriceLog        0     8
#>  9: -1.3408109 -2.1245834  0.01         1 TF_GoldsteinPriceLog        0     9
#> 10: -2.1225452 -1.3408109  0.01         1 TF_GoldsteinPriceLog        0    10
#>     batch
#>     <num>
#>  1:     1
#>  2:     1
#>  3:     1
#>  4:     1
#>  5:     1
#>  6:     1
#>  7:     1
#>  8:     1
#>  9:     1
#> 10:     1
opt$objective$archive
#>                       x       fval                  grad     gnorm
#>                  <list>      <num>                <list>     <num>
#>  1:           0.22,0.77  1.2102644   0.1009067,5.1402328  5.141223
#>  2: 0.2189909,0.7185977  0.9157526     0.801070,6.372357  6.422511
#>  3: 0.2109802,0.6548741  0.4217145     2.656552,8.997572  9.381555
#>  4: 0.1844147,0.5648984 -0.6741307   -3.381065, 4.254834  5.434631
#>  5: 0.2182254,0.5223500 -0.9818620   -8.098642, 1.183078  8.184600
#>  6: 0.2992118,0.5105193 -0.9876309    3.667496,15.072102 15.511892
#>  7: 0.2625368,0.3597982 -1.1017546   -7.800819,-5.088128  9.313529
#>  8: 0.3405450,0.4106795 -2.1680122 -0.4281407, 2.0881313  2.131571
#>  9: 0.3448264,0.3897982 -2.1245834   -6.443313,-7.157191  9.630247
#> 10: 0.4092595,0.4613701 -1.3408109     3.640808,7.028256  7.915293

Visualize Optimization Traces

A layer of the Visualizer class is $add_optimization_trace() that gets the optimizer as argument and adds the optimization trace to the plot:

viz = as_visualizer(obj, type = "surface")
viz$add_optimization_trace(opt)
viz$plot()

Step size control

When calling $optimize(), the second argument is stepSizeControl that allows to expand or compress the update added to the old value of xx. For example, for GD with xnew=xold+lr*Δf(xold)x_{\text{new}} = x_{\text{old}} + lr * \Delta_f(x_{\text{old}}) the update u=lr*Δf(xold)u = lr * \Delta_f(x_{\text{old}}) is multiplied with the return value of stepSizeControl(). There are a few pre-implemented control functions like line search or various decaying methods:

  • stepSizeControlLineSearch(lower, upper): Conduct a line search for aa in xnew=xold+a*lr*Δf(xold)x_{\text{new}} = x_{\text{old}} + a * lr * \Delta_f(x_{\text{old}})`.
  • stepSizeControlDecayTime(decay): Lower the updates by (1+decay*iteration)−1(1 + decay * iteration)^{-1}.
  • stepSizeControlDecayExp(decay): Lower the updates by exp(−decay*iteration)exp(-decay * iteration).
  • stepSizeControlDecayLinear(iter_zero): Lower the updates until iter_zero is reached. Updates with iter > iter_zero are 0.
  • stepSizeControlDecaySteps(drop_rate, every_iter): Lower the updates every_iter by drop_rate.

Note that these functions return a function that contains a function with the required signature:

stepSizeControlDecayTime()
#> function (x, u, obj, opt) 
#> {
#>     assertStepSizeControl(x, u, obj, opt)
#>     epoch = nrow(obj$archive)
#>     return(1/(1 + decay * epoch))
#> }
#> <bytecode: 0x56222cb89618>
#> <environment: 0x56222cb88c40>

Let’s define multiple gradient descent optimizers and optimize 10 steps with a step size control:

x0 = c(0.22, 0.77)
lr = 0.01

oo1 = OptimizerGD$new(obj, x_start = x0, lr = lr, id = "GD without LR Control", print_trace = FALSE)
oo2 = OptimizerGD$new(obj, x_start = x0, lr = lr, id = "GD with Line Search", print_trace = FALSE)
oo3 = OptimizerGD$new(obj, x_start = x0, lr = lr, id = "GD with Time Decay", print_trace = FALSE)
oo4 = OptimizerGD$new(obj, x_start = x0, lr = lr, id = "GD with Exp Decay", print_trace = FALSE)
oo5 = OptimizerGD$new(obj, x_start = x0, lr = lr, id = "GD with Linear Decay", print_trace = FALSE)
oo6 = OptimizerGD$new(obj, x_start = x0, lr = lr, id = "GD with Step Decay", print_trace = FALSE)

oo1$optimize(steps = 10)
oo2$optimize(steps = 10, stepSizeControlLineSearch())
oo3$optimize(steps = 10, stepSizeControlDecayTime())
oo4$optimize(steps = 10, stepSizeControlDecayExp())
oo5$optimize(steps = 10, stepSizeControlDecayLinear())
oo6$optimize(steps = 10, stepSizeControlDecaySteps())

For now we don’t know how well it worked. Let’s collect all archives with mergeOptimArchives() and visualize the step sizes and function values with patchwork magic:

arx = mergeOptimArchives(oo1, oo2, oo3, oo4, oo5, oo6)

library(ggplot2)
library(patchwork)
gg1 = ggplot(arx, aes(x = iteration, y = step_size, color = optim_id))
gg2 = ggplot(arx, aes(x = iteration, y = fval_out, color = optim_id))

(gg1 + ggtitle("Step sizes") |
  gg1 + ylim(0, 1) + ggtitle("Step sizes (zoomed)") |
  gg2 + ggtitle("Objective")) +
  plot_layout(guides = "collect") &
  geom_line() &
  theme_minimal() &
  theme(legend.position = "bottom") &
  ggsci::scale_color_simpsons()
#> Warning: Removed 2 rows containing missing values or values outside the scale range
#> (`geom_line()`).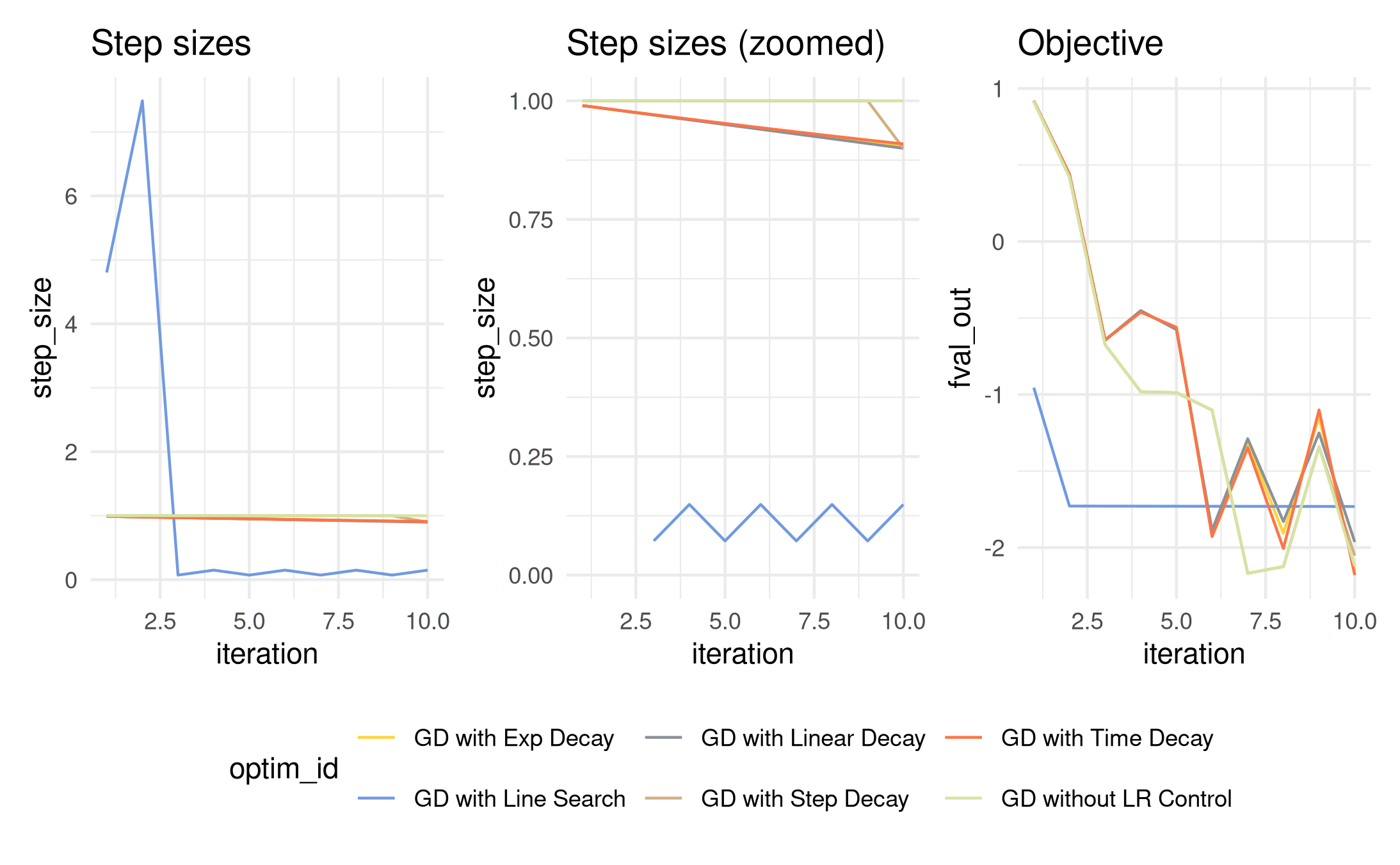

Visualizing the traces is done as before by adding optimization trace layer. We can do this for all optimizers to add multiple traces to the plot:

viz = as_visualizer(obj, type = "surface")

viz$add_optimization_trace(oo1)
viz$add_optimization_trace(oo2)
viz$add_optimization_trace(oo3)
viz$add_optimization_trace(oo4)
viz$add_optimization_trace(oo5)
viz$add_optimization_trace(oo6)

viz$plot()

Practically, it should be no issue to also combine multiple control functions. The important thing is to keep the signature of the function by allowing the function to get the arguments x (current value), u (current update), obj (Objective object), and opt (Optimizer object):

myStepSizeControl = function(x, u, obj, opt) {
  sc1 = stepSizeControlLineSearch(0, 10)
  sc2 = stepSizeControlDecayTime(0.1)
  return(sc1(x, u, obj, opt) * sc2(x, u, obj, opt))
}

my_oo = OptimizerGD$new(obj, x_start = x0, lr = lr, id = "GD without LR Control", print_trace = FALSE)
my_oo$optimize(100, myStepSizeControl)
tail(my_oo$archive)
#>        x_out      x_in                      update  fval_out   fval_in    lr
#>       <list>    <list>                      <list>     <num>     <num> <num>
#> 1: 0.50,0.25 0.50,0.25  4.440892e-10,-3.996803e-09 -3.129126 -3.129126  0.01
#> 2: 0.50,0.25 0.50,0.25 -2.664535e-09,-7.105427e-09 -3.129126 -3.129126  0.01
#> 3: 0.50,0.25 0.50,0.25 -3.552714e-09,-3.552714e-09 -3.129126 -3.129126  0.01
#> 4: 0.50,0.25 0.50,0.25   8.881784e-10,7.549517e-09 -3.129126 -3.129126  0.01
#> 5: 0.50,0.25 0.50,0.25  0.000000e+00,-1.021405e-08 -3.129126 -3.129126  0.01
#> 6: 0.50,0.25 0.50,0.25   8.881784e-10,0.000000e+00 -3.129126 -3.129126  0.01
#>      step_size         objective_id momentum  step batch
#>          <num>               <char>    <num> <int> <num>
#> 1: 0.015061886 TF_GoldsteinPriceLog        0    95     1
#> 2: 0.006942669 TF_GoldsteinPriceLog        0    96     1
#> 3: 0.010225887 TF_GoldsteinPriceLog        0    97     1
#> 4: 0.063947308 TF_GoldsteinPriceLog        0    98     1
#> 5: 0.006044013 TF_GoldsteinPriceLog        0    99     1
#> 6: 0.564836746 TF_GoldsteinPriceLog        0   100     1

Optimization traces

Let’s optimize a custom linear model objective (TODO: see objective_functions vignette) using the three available optimizers.

# Define the linear model loss function as SSE:
l2norm = function(x) sqrt(sum(crossprod(x)))

mylm = function(x, Xmat, y) {
  l2norm(y - Xmat %*% x)
}
# Use the iris dataset with response `Sepal.Width` and feature `Petal.Width`:
Xmat = model.matrix(~Petal.Width, data = iris)
y = iris$Sepal.Width

# Create a new object:
obj_lm = Objective$new(id = "iris LM", fun = mylm, xdim = 2, Xmat = Xmat, y = y, minimize = TRUE)

oo1 = OptimizerGD$new(obj_lm, x_start = c(0, -0.05), lr = 0.001, print_trace = FALSE)
oo2 = OptimizerMomentum$new(obj_lm, x_start = c(-0.05, 0), lr = 0.001, print_trace = FALSE)
oo3 = OptimizerNAG$new(obj_lm, x_start = c(0, 0), lr = 0.001, print_trace = FALSE)

oo1$optimize(steps = 100)
oo2$optimize(steps = 100)
oo3$optimize(steps = 100)

As shown previously, optimization traces can be added by $add_optimization_trace.

viz = as_visualizer(obj_lm, x1_limits = c(-0.5, 5), x2_limits = c(-3.2, 2.8), type = "surface")


viz$add_optimization_trace(oo1, add_marker_at = round(seq(1, 100, len = 10L)))
viz$add_optimization_trace(oo2, add_marker_at = c(1, 50, 90), marker_shape = c("square", "diamond", "cross"))
viz$add_optimization_trace(oo3, add_marker_at = 100, marker_shape = "diamond-open")

viz$plot()

Using the alternative ggplot2 backend makes sense when further customization is desired (TODO see advanced_visualization vignette):

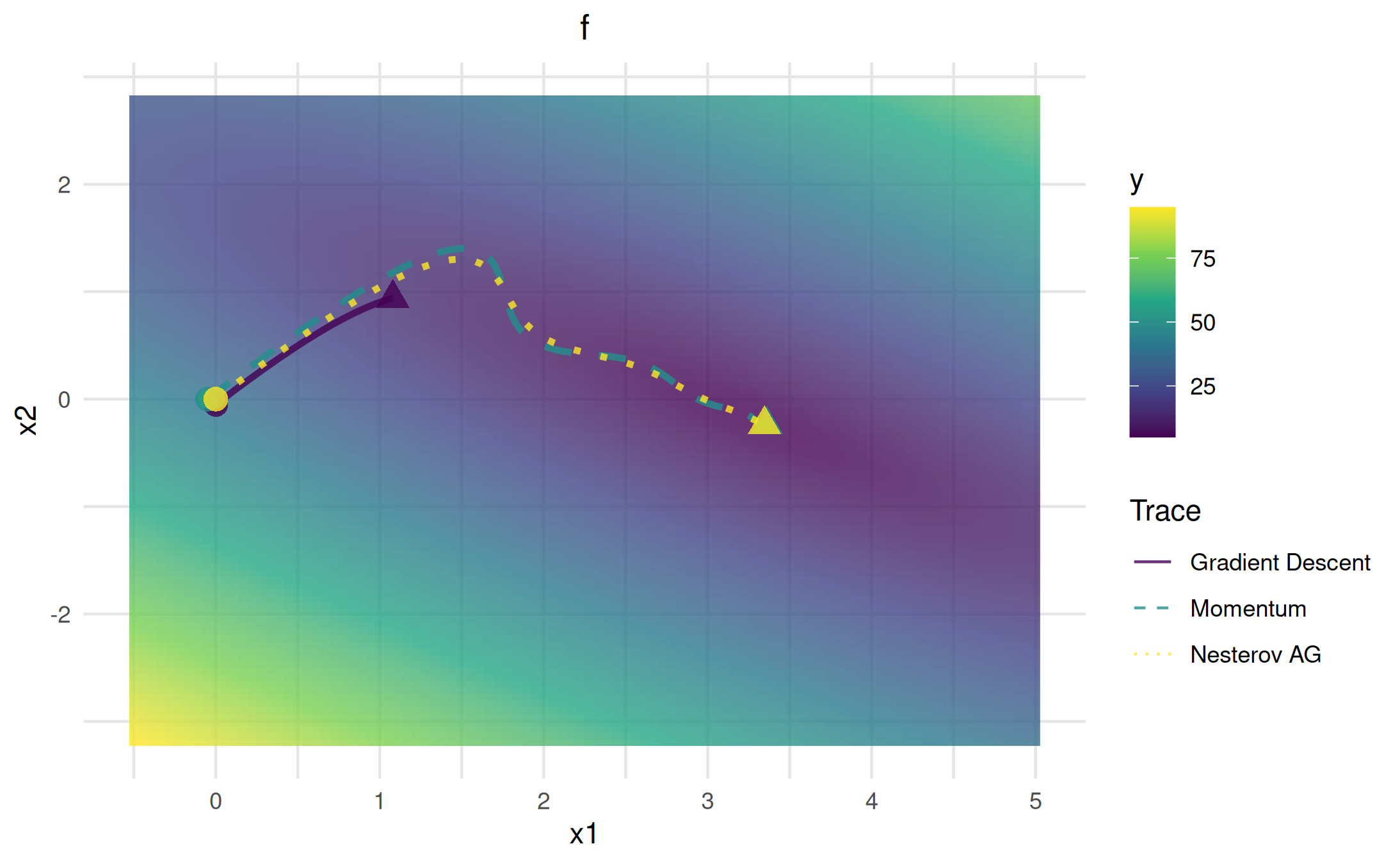
viz_2d = as_visualizer(obj_lm, x1_limits = c(-0.5, 5), x2_limits = c(-3.2, 2.8))

viz_2d$add_optimization_trace(oo1,
  name = "Gradient Descent"
)

viz_2d$add_optimization_trace(oo2,
  line_type = "dashed",
  name = "Momentum"
)

viz_2d$add_optimization_trace(oo3,
  line_type = "dotted",
  name = "Nesterov AG"
)

viz_2d$plot()